칼슘(Ca)의 밀도 계산. 입방 최조밀 쌓임 구조 fcc 원자 반지름 197 pm

고체 칼슘은 입방 최조밀 쌓임 구조를 가지고 있다.

칼슘의 원자 반지름을 197 pm라고 가정하고,

고체 칼슘의 밀도를 계산하라.

단, Ca의 몰질량 = 40.08 g/mol

Calcium has a cubic closest packed structure as a solid.

Assuming that calcium has an atomic radius of 197 pm,

calculate the density of solid calcium.

---------------------------------------------------

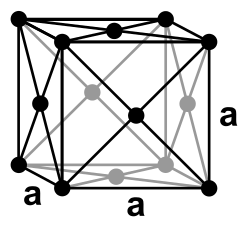
A cubic closest packed structure contains a fcc unit cell.

---> 단위세포에 있는 원자의 개수 = 4개 (4 atoms)

( 참고 https://ywpop.tistory.com/12440 )

[ 그림 출처 Wikimedia ] face-centered cubic unit cell.

단위세포의 질량, mass of unit cell

= (4 atoms) (40.08 g/mol) (1 mol / 6.022×10^23 atoms)

= (4) (40.08) (1 / (6.022×10^23))

= 2.66224×10^(-22) g

a = 4r / sqrt(2)

> a: edge length (단위세포의 모서리 길이)

> r = radius (원자 반지름)

( 참고 https://ywpop.tistory.com/12439 )

= (4×197) / sqrt(2)

= 557.2 pm

= 557.2×10^(-10) cm

단위세포의 밀도, density of unit cell

= 질량 / 부피

= (2.66224×10^(-22) g) / (557.2×10^(-10) cm)^3

= (2.66224×10^(-22)) / (557.2×10^(-10))^3

= 1.5389 g/cm3

또는

d = [Z × M] / [a^3 × N_A]

> d: 밀도 (g/cm3)

> Z: 단위세포에 있는 원자의 개수 (개)

> M: 몰질량 (g/mol)

> a: edge length (cm)

> N_A: 6.022×10^23 (개/mol)

= [4 × 40.08] / [(557.2×10^(-10))^3 × (6.022×10^23)]

= 1.5389 g/cm3

답: 1.54 g/cm3

은(Ag)의 밀도 계산. 입방 조밀 쌓임 구조 fcc 원자 반지름 144 pm

[키워드] 금속 칼슘의 밀도 기준, 금속 Ca의 밀도 기준, fcc 기준, fcc dic, 고체화학 기준, 고체화학 사전

칼슘(Ca)의 밀도 계산. 입방 최조밀 쌓임 구조 fcc 원자 반지름 197 pm